# Lecture 14 - AI Pathfinding ### SET09121 - Games Engineering <br /><br /> Leni Le Goff <br /> School of Computing. Edinburgh Napier University --- # Recommended Reading - Artificial Intelligence for Games. Second Edition. Millington and Funge (2009). - Whole chapter on pathfinding.  --- ## Pathfinding  --- # What is Pathfinding? - Pathfinding (or more specifically path planning) is a decision making process that feeds into the movement. - You can consider it as crossing the boundary between movement and decision making. - Pathfinding is really the key ingredient that allows characters to navigate. - There is a good chance you have covered this before in AI or Algorithms and Data Structures. --- # Why do we need Pathfinding? - Game maps are generally too complicated for simple steering to be in charge. - We could hard-code routes through the map, but that is not a scalable strategy. - So we need a technique that allows an entity to determine a route to follow to get to its destination. - Pathfinding allows us to do this - it examines map data and provides a set of waypoints to follow by the entity. - Pathfinding is just a form of graph search, and there are different methods to do this. - We need a fast solution - A* being the most commonly used. --- # Why Too Complicated? - If there are only simple convex objects, basic avoidance behaviours will look great! - But if you have concavities, obstacle avoidance will not work - As we discussed previously, level design impacts AI design --- # Pathfinding Costs - Maps are very big today - some over $100km^2$. - If each square metre was a navigation point that's $10^8$ points. - If we can travel in any direction, things get very expensive. - Generally we are looking for simplifications to combat this.  <!-- .element width="40%" --> --- ## Underpinning Theory - Graphs  --- # What is a Graph? - A **graph** ***G***, is a set of **nodes** (vertices or points) ***V*** connected by **edges** (links or lines) ***E***: $$G = (V,E)$$ - From a game pathfinding point of view, a node is a location in the game world, and an edge is a path between two edges. --- # Weighted Graphs - For pathfinding we are concerned with the cost. - The cost of a path is dependent on some factors that allows us to determine what the cheapest path is. - Game factors: distance, underlying terrain, obstacles - We consider that an edge has a cost associated with it (weight) - To traverse an edge means to incur the cost of that traversal.  <!-- .element width="60%" --> --- # Directed Graphs - A graph may also be directed. - This means that an edge only has one direction of travel. - We won't use this, but it does exist in games. - For example, jumping down a ledge you cannot get back up.  <!-- .element width="60%" --> --- # Tile Engine and Graphs - We will be building our pathfinding into our tile engine. - It is just easier - the data is all there. - We will use the data directly and build up our path incrementally from the level data. - The algorithm should be reusable though - you just need to specify where you are getting the data from. 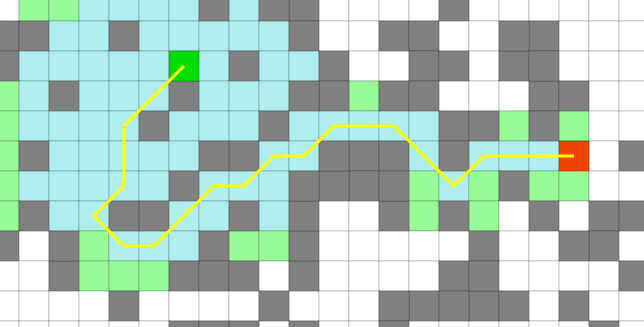 <!-- .element width="60%" --> --- # Tile Graphs - This approach should be OK for anything you are building, but a word of warning... - A tile-based graph pathfinding approach does not scale to large maps. - We mentioned this at the start. - A worst case pathfind means that all paths on all nodes have to be searched. - This leads to an algorithmic complexity of $\mathcal{O}(\lvert V \rvert^2)$. - $\lvert V \rvert$ is the size of the node (vertex) set. - So don't convert your massive million by million tile world into a pathfinding nightmare. --- ## Dijkstra --- # Dijkstra's Algorithm - Defined by Edsger Dijkstra in 1956. - An algorithm to find the shortest path between two nodes in a graph. - For a game, find the shortest path between two locations. - An extension to the algorithm allowed finding of all the paths from a source node. - In other words, how do we get to each of the nodes in the shortest time. - This algorithm is not only used for pathfinding in games. - Google Maps will use something similar for moving in road networks. - Network routing protocols will use such an algorithm. - Dijkstra is typically too expensive to use in games --- # Dijkstra's Algorithm - 6 steps 1. Mark all nodes as initially unvisited. Use this to create the set of *unvisited* nodes. 2. Set costs for the nodes: - Initial node (current node) cost is 0. - Other node costs set to infinity. 3. For the current node look at connected neighbours. Use to determine a tentative cost from the current node. Update the neighbours costs if the new route is shorter. 4. Mark current node as visited (remove from *unvisited* set). We will not visit this node again. 5. If destination has been marked visited (in other words we reached our destination) or all *unvisited* nodes have infinite cost, stop. 6. Else select unvisited node with smallest tentative cost from the initial node and set as current node. Go to step 3. --- 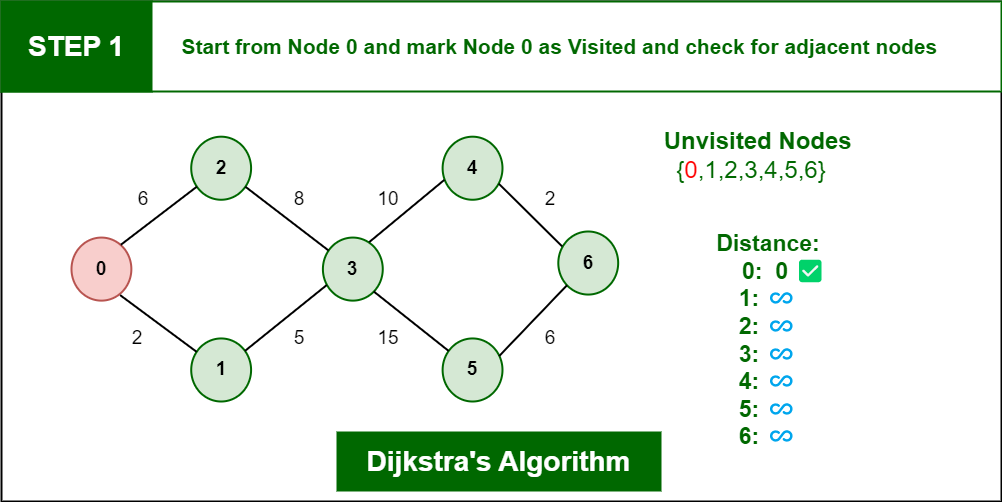<!-- .element width="100%" height="100%" --> [source](https://www.geeksforgeeks.org/dsa/introduction-to-dijkstras-shortest-path-algorithm/) --- 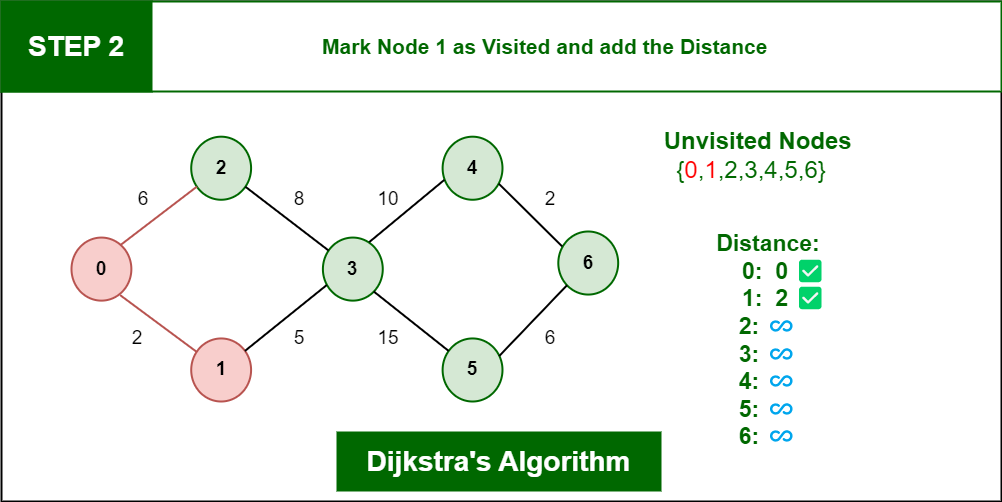<!-- .element width="100%" height="100%" --> [source](https://www.geeksforgeeks.org/dsa/introduction-to-dijkstras-shortest-path-algorithm/) ---  <!-- .element width="100%" height="100%" --> [source](https://www.geeksforgeeks.org/dsa/introduction-to-dijkstras-shortest-path-algorithm/) --- <!-- .element width="100%" height="100%" --> [source](https://www.geeksforgeeks.org/dsa/introduction-to-dijkstras-shortest-path-algorithm/) --- 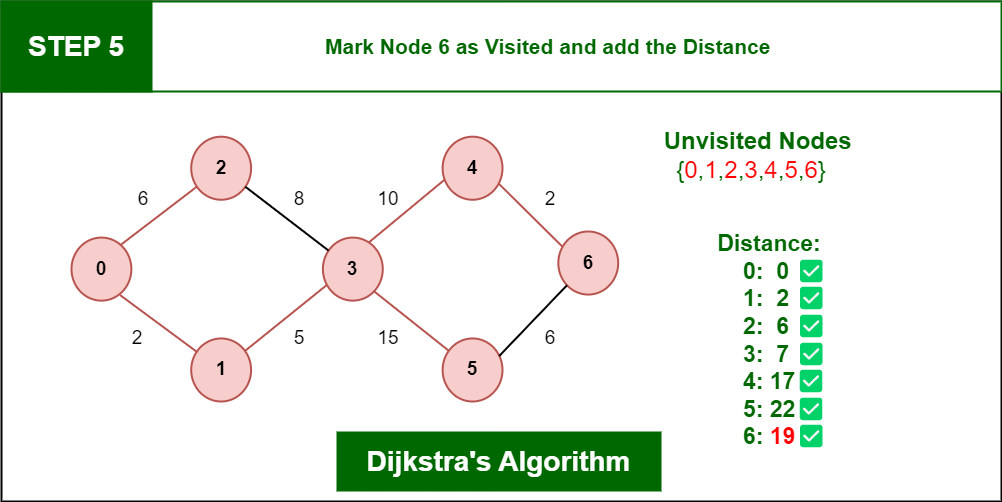<!-- .element width="100%" height="100%" --> [source](https://www.geeksforgeeks.org/dsa/introduction-to-dijkstras-shortest-path-algorithm/) --- # Dijkstra's Algorithm - Dijkstra guarantees that the path found is going to be the shortest - Unlike approaches such as best-first search (BFS), depth-first search - BFS: special case of Dijkstra without weights or priority queue - Dijkstra iterates through nodes based on which one has the shortest distance from the start node. - This means it is not actively searching for the destination but doing a traversal of the graph until it happens to find it. --- # Example - Dijkstra at Work <iframe width="1400" height="800" src="https://www.youtube.com/embed/dhvf9KCAsVg" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""></iframe> --- # Problems with Dijkstra - The problem with Dijkstra's algorithm is it not actually searching for our destination. - Dijkstra's approach sets out to find the shortest path from a source to the neighbouring nodes. - It just might run into the destination at this step. - Therefore, Dijkstra is expensive for pathfinding - it might just get lucky. - This leads to an algorithmic complexity of $\mathcal{O}(\lvert V \rvert^2)$. - So we need a better technique that tries to find our destination node. --- # Dijkstra for many entities going to the same place - What if all your agents are only pathing to a single location? - E.g. enemies swarming the player - If so, then you can precalculate it and have hundreds of agents! - Precalculate the costs to the goal(s) using Dijkstra from any point in the map - E.g. goal is player position - When calculating the path, for each agent: - Look at cost at current position - Look at costs at neighbouring positions - Pick the neighbour position with lower cost - Not needed for this module, but it's food for thought! --- ## A* --- # A* - A* was first described in 1968 (about 10 years after Dijkstra's algorithm) by a team from the Stanford Research Institute. - A* is called a best-first search or an informed-search algorithm. - This is because it takes into account a goal for working out which node to select next. - In a game our goal is the destination we want to get to quickest. - It does this by determining a cost for a node traversal based on whether it best meets the goal. - We can use different heuristics to evaluate these costs. - We will just use Euclidean (straight-line) distance. --- # A* Similarity to Dijkstra - Dijkstra is a special case of A*, where the heuristic is zero - The algorithm is identical to Dijkstra, except a few points: - The cost is computed as a *combined cost*: $$C(n) = g(n) + h(n)$$ - Where - h: heuristic function calculating the cost from the current node to the goal node - g: tentative cost from start to current node - C: the combined cost --- # A* - As stated, A* is a best-first search algorithm. - This means it doesn't select a shortest path from where it is, but chooses a node that looks like a better choice towards the goal. - However, in the worst-case A* still might have to search the entire graph. - We still have $\mathcal{O}(\lvert V \rvert^2)$ complexity.  <!-- .element width="40%" --> --- # Example - A* at Work <iframe width="1400" height="800" src="https://www.youtube.com/embed/19h1g22hby8" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""></iframe> --- # Heuristics The most common heuristics used are distances . - **Euclidean distance** (straight line): $$ h(n) = \sqrt{ (x_g-x_n)^2 + (y_g-y_n)^2 } $$ - **Manhattan distance**: $$ h(n) = \lvert x_g-x_n \rvert + \lvert y_g-y_n \rvert $$ - **Chebyshev distance**: $$ h(n) = \max(\lvert x_g-x_n \rvert , \lvert y_g-y_n \rvert) $$ With $n$ current node and $g$ goal node --- # Heuristics  <!-- .element width="100%" height=100%" --> --- # A* versus Dijkstra <iframe width="1400" height="800" src="https://www.youtube.com/embed/g024lzsknDo" frameborder="0" allow="accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture" allowfullscreen=""></iframe> --- ## Pathfinding and Steering --- # Output from Pathfinding - The output from a path finding or a path planning operation is called a *path* or *walk*. - There are different approaches we can take in a game: - A series of directions of travel (useful for discrete movement). - A list of nodes to visit (better for continuous movement). - We will take the latter approach.  <!-- .element width="40%" --> --- # Pathfinding and Steering - Our aim is to use pathfinding as a decision making process for our movement. - The basic idea is that we have a starting position and a target position. - We use pathfinding to plan the sequence of movements to reach the target position. - The list of nodes to visit then allows us to traverse the map using a steering behaviour. - The simplest approach is just to use an arrive behaviour for each node. Seeking might cause bouncing. - Combining steering behaviours, pathfinding, and physics will give you all the movement behaviour you need. --- # Other Techniques - We have only looked at the main technique used in games but there are other considerations. - Jump Point Search: optimisation to A* for uniform-cost grids - Algorithm considers "jumps" along straight lines in the grid - HPA\* and [HAA*](https://web.archive.org/web/20190411040123/http://aigamedev.com/open/article/clearance-based-pathfinding/) : hierarchical variants - Break map into chunks, identify chunk entries/exits, precompute paths per chunk and run a multi-resolution search at runtime  <!-- .element width="40%" --> --- # Summary - We've only covered the basics of pathfinding, but this is enough for what you need. - Pathfinding is really about finding the least expensive path to a destination. - This can obviously change based on the map changing. - Our use of pathfinding will get a list of nodes to visit and the subsequent use of this information to move a character around. - The lab will provide you with an algorithm that will work in the tile engine, but you should be able to extract the core idea if you need to.